Принцип максимального правдоподобия (maximum likelihood)

Заметим, прежде всего, что второй член в правой части выражения не зависит от данных. Первый же, отражающий эмпирический опыт, как правило, имеет вид колокола тем более узкого, чем больше объем имеющихся в распоряжении данных (см. рисунок 3.4).

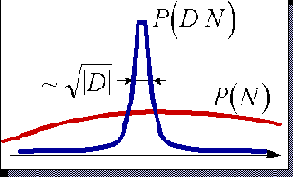
Рис. 3.4. Качественная зависимость априорной и эмпирической составляющих формулы Байеса. Чем больше данных - тем точнее можно выбрать проверяемую гипотезу

Действительно, чем больше данных - тем точнее может быть проверены следствия конкурирующих гипотез, и, следовательно, тем точнее будет выбор наилучшей.

Следовательно, при стремлении количества данных к бесконечности, последним членом можно пренебречь. Это приближение:

получило название принципа максимального правдоподобия (Фишер) и характерно для т.н. параметрической статистики, в которой модель представляет собой семейство решений с небольшим и фиксированным набором параметров.

Отрицательный логарифм вероятности имеет смысл эмпирической ошибки при подгонке данных с помощью имеющихся в моделе свободных параметорв.

Например, в задаче аппроксимации функций обычно предполагается, что данные порождаются некоторой неизвестной функцией, которую и надо восстановить, но их "истинные" значения искажены случайным гауссовым шумом. Таким образом, условная вероятность набора данных

для модели

, зависящей от настраиваемых параметров w, имеет гауссово распределение:

Отрицательный логарифм, таким образом, пропорционален сумме квадратов, и аппроксимация функции сводится к минимизации среднеквадратичной ошибки:

Содержание раздела