Алгоритм Кохонена

В 1982 году финский ученый Тойво Кохонен (Kohonen, 1982) предложил ввести в базовое правило соревновательного обучения информацию о расположении нейронов в выходном слое. Для этого нейроны выходного слоя упорядочиваются, образуя одно- или двумерные решетки. Т.е. теперь положение нейронов в такой решетке маркируется векторным индексом

Такое упорядочение естественым образом вводит расстояние между нейронами

в слое. Модифицированное Кохоненым правило соревновательного обучения учитывает расстояние нейронов от нейрона-победителя:

Функция соседства

равна единице для нейрона-победителя с индексом

и постепенно спадает с расстоянием, например по закону

. Как темп обучения

, так и радиус взаимодействия нейронов

постепенно уменьшаются в процессе обучения, так что на конечной стадии обучения мы возвращаемся к базовому правилу адаптации весов только нейронов-победителей.

В отличае от "газо-подобной" динамике обучения при индивидуальной подстройке прототипов (весов нейронов), обучение по Кохонену напоминает натягивание эластичной сетки прототипов на массив данных из обучающей выборки. По мере обучения эластичность сети постепенно увеличивается, чтобы не мешать окончательной тонкой подстройке весов.

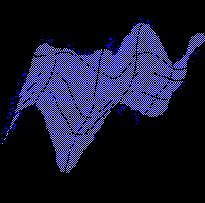
Рис. 4.12. Двумерная топографическая карта набора трехмерных данных. Каждая точка в трехмерном пространстве попадает в свою ячейку сетки имеющую координату ближайшего к ней нейрона из двумерной карты

В результате такого обучения мы получаем не только квантование входов, но и упорядочивание входной информации в виде одно- или двумерной карты. Каждый многомерный вектор имеет свою координату на этой сетке, причем чем ближе координаты двух векторов на карте, тем ближе они и в исходном пространстве. Такая топографическая карта дает наглядное представление о структуре данных в многомерном входном пространстве, геометрию которого мы не в состоянии представить себе иным способом. Визуализация многомерной информации является главным применением карт Кохонена.

Заметим, что в согласии с общим житейским принципом "бесплатных обедов не бывает", топографические карты сохраняют отношение близости лишь локально: близкие на карте области близки и в исходном пространстве, но не наоборот (рисунок 4.13). В общем случае не существует отображения, понижающего размерность и сохраняющего отношения близости глобально.

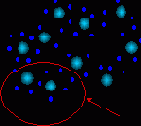
Рис. 4.13. Пример одномерной карты двумерных данных. Стрелкой показана область нарушения непрерывности отображения: близкие на плоскости точки отображаются на противоположные концы карты

Удобным инструментом визуализации данных является раскраска топографических карт, аналогично тому, как это делают на обычных географических картах. Каждый признак данных порождает свою раскраску ячеек карты - по величине среднего значения этого признака у данных, попавших в данную ячейку.

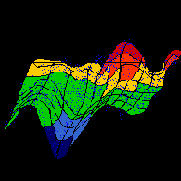
Рис. 4.14. Раскраска топографической карты, индуцированная i-ой компонентой входных данных

Собрав воедино карты всех интересующих нас признаков, получим топографический атлас, дающий интегральное представление о структуре многомерных данных. Далее в этой книге мы рассмотрим практическое применение этой методики к анализу балансовых отчетов и предсказанию банкротств.

Содержание раздела