Оценка вычислительной сложности обучения

В этой лекции мы рассмотрели два разных типа обучения, основанные на разных принципах кодирования информации выходным слоем нейронов. Логично теперь сравнить их по степени вычислительной сложности и выяснить когда выгоднее применять понижение размерности, а когда - квантование входной информации.

Как мы видели, алгоритм обучения сетей, понижающих размерность, сводится к обычному обучению с учителем, сложность которого была оценена ранее. Такое обучение требует

операций, где

- число синаптических весов сети, а

- число обучающих примеров. Для однослойной сети с

входами и

выходными нейронами число весов равно

и сложность обучения

можно оценить как

, где

- коэффициент сжатия информации.

Кластеризация или квантование требуют настройки гораздо большего количества весов - из-за неэффективного способа кодирования. Зато такое избыточное кодирование упрощает алгоритм обучения. Действительно, квадратичная функция ошибки в этом случае диагональна, и в принципе достижение минимума возможно за

шагов (например в пакетном режиме), что в данном случае потребует

операций. Число весов, как и прежде, равно

, но степень сжатия информации в данном случае определяется по-другому:

. Сложность обучения как функция степени сжатия запишется в виде:

При одинаковой степени сжатия, отношение сложности квантования к сложности данных снижения размерности запишется в виде:

Рисунок 4.11 показывает области параметров, при которых выгоднее применять тот или иной способ сжатия информации.

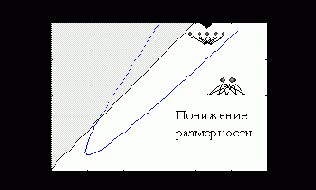
Рис. 4.11. Области, где выгоднее использовать понижение размерности или квантование

Наибольшее сжатие возможно методом квантования, но из-за экспоненциального роста числа кластеров, при большой размерности данных выгоднее использовать понижение размерности. Максимальное сжатие при понижении размерности равно

, тогда как квантованием можно достичь сжатия

(при двух нейронах-прототипах). Область недостижимых сжатий

показана на рисунке серым.

В качестве примера рассмотрим типичные параметры сжатия изображений в формате JPEG.
При этом способе сжатия изображение разбивается на квадраты со стороной

пикселей, которые и являются входными векторами, подлежащими сжатию. Следовательно, в данном случае

. Предположим, что картинка содержит

градаций серого цвета, т.е. точность представления данных

. Тогда координата абсциссы на приведенном выше графике будет

. Как следует из графика при любых допустимых степенях сжатия в данном случае оптимальным с точки зрения вычислительных затрат является снижение

размерности. 1)

Однако, при увеличении размеров элементарного блока, появляется область высоких степеней сжатия, достижимых лишь с использованием квантования. Скажем, при

, когда

, в соответствии с графиком (см. рисунок 4.11), квантование следует применять для сжатия более

, т.е.

.

Содержание раздела