Правило обучения Ойа

От этого недостатка, однако, можно довольно просто избавиться, добавив член, препятствующий возрастанию весов. Так, правило обучения Ойа:

или в векторном виде:

максимизирует чувствительность выхода нейрона при ограниченной амплитуде весов. В этом легко убедиться, приравняв среднее изменение весов нулю. Умножив затем правую часть на w, видим, что в равновесии:

. Таким образом, веса обученного нейрона расположены на гипер-сфере:

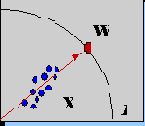
Рис. 4.3. При обучении по правилу Ойа, вектор весов нейрона располагается на гипер-сфере в направлении, максимизирующем проекцию входных векторов

Отметим, что это правило обучения по существу эквивалентно дельта-правилу, только обращенному назад - от входов к выходам (т.е. при замене

). Нейрон как бы старается воспроизвести значения своих входов по заданному выходу. Тем самым, такое обучение стремится максимально повысить чувствительность единственного выхода-индикатора к многомерной входной информации, являя собой пример оптимального сжатия информации.

Эту же ситуацию можно описать и по-другому. Представим себе персептрон с одним (здесь - линейным) нейроном на скрытом слое, в котором число входов и выходов совпадает, причем веса с одинаковыми индексами в обоих слоях одинаковы. Будем учить этот персептрон воспроизводить в выходном слое значения своих выходов. При этом, дельта-правило обучения верхнего (а тем самым и нижнего) слоя примет вид правила Ойа:

Рис. 4.4. Автоассоциативная сеть с узким горлом - аналог правила обучения Ойа

Таким образом, существует определенная параллель между самообучающимися сетями и т.н. автоассоциативными сетями, в которых учителем для выходов являются значения входов. Подобного рода нейросети с узким горлом также способны осуществлять сжатие информации.

Содержание раздела