Нейрокомпьютинг и его применения в экономике и бизнесе
Версии протитипа
Итак, структура аттракторов в модели Хопфилда может допускать различные содержательные интерпретации. В том случае, когда она совпадает со структурой запоминаемых образов мы говорим об ассоциативной памяти (пассивной). Если, напротив, в сети формируется единственный аттрактор, в каком-то смысле являющийся прототипом этих образов, то проявляется способность сети к обобщению (generalization). В общем же случае структура аттракторов сети настолько сложна, что на первый взгляд не допускает какой-либо наглядной трактовки. Действительно, такая трактовка должна быть настолько универсальной, чтобы включать режимы запоминания и обобщения в качестве предельных случаев. Тем не менее она возможна и опирается на рассуждения, которые приводятся в данном разделе.
Начнем с рассмотрения сети Хопфилда, в память которой, согласно правилу Хебба, записан только один образ


У такой сети есть только два зеркально симметричных стационарных состояния


Заметим, что все связи в сети дают в энергию одинаковый отрицательный вклад и поэтому являются не фрустрированными. Напомним, что условием фрустрации связи в состоянии сети является неравенство

Именно это условие не выполняется ни для одной связи в сети с записанным единственным образом. Мы можем трактовать подобную ситуацию так, что сеть с одним записанным в нее образом точно воспроизводит его в виде своего аттрактора (с точностью до зеркального отражения), и если мы выберем в этой сети случайную связь, то вероятность ее фрустрации будет равна нулю.
Таким образом, сеть Хопфилда идеально приспособлена для хранения единственного образа.
Рассмотрим теперь следующую систему (см. рисунок 5.6). Пусть в Хопфилдовской сети-передатчике (слева) записан единственный образ


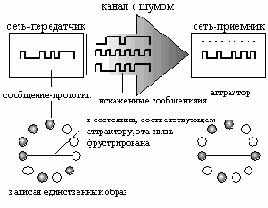
Внизу: сети с записанным единственным сообщением прототипом (слева) и со всеми искаженными версиями этого сообщения (справа)" width="313" height="243">
Рис. 5.6. Вверху: интерпретация стационарных состояний в сети Хопфилда как локально наиболее правдоподобных версий сообщения, многократно переданного сетью-передатчиком в сеть-приемник через канал с шумом. Внизу: сети с записанным единственным сообщением прототипом (слева) и со всеми искаженными версиями этого сообщения (справа)
Задача сети-премника состоит в том, чтобы имея P полученных сообщений






Вспоминая выражение для правила Хебба, убеждаемся что если сообщения


Используя последнее соотношение, преобразуем выражение для энергии состояния в сети-приемнике к виду

Поскольку мы не знаем точного вида сообщения



Таким образом, энергия состояния сети-приемника с точностью до постоянных множителя и слагаемого совпадает с вероятностью фрустрации случайно выбранной связи в сети-передатчике, оцененной по полученным от нее сообщениям.
Однако в сети-передатчике записано лишь одно сообщение, и вероятность фрустрации связей в ней равна нулю. Но поскольку ни сообщение, ни соответствующие ему связи сети-передатчика нам не известны, мы можем лишь пытаться найти такое состояние сети-приемника, которое хотя бы локально минимизирует эту вероятность. Подобные состояния были бы локально наилучшими версиями сообщения, посылаемого сетью-передатчиком.
А так как вероятность нахождения фрустрированной связи в передатчике связана с энергией состояния в приемнике, то такими наилучшими версиями как раз и окажутся состояния, соответствующие энергетическим минимумам сети-приемника. Таким образом все аттракторы сети Хопфилда, связи которой сформированы согласно правилу Хебба, исходя из набора обучающих векторов

Подобный подход устраняет деление состояний памяти на истинные и ложные, давая им единую интерпретацию. В такой трактовке функционирование сети Хопфилда в качестве пассивной памяти соответствует случаю, когда шум в канале очень велик, т.е. все принимаемые сетью сообщения некоррелированы. Это не дает ей возможности выделить из них сообщения и, рассматривая их как равноправные его версии, сеть генерирует аттрактор в каждой точке N-мерного пространства

Хотя первоначально сеть Хопфилда привлекалась для объяснения свойств ассоциативной памяти, можно привести множество различных примеров ее применения и для выделения зашумленного сигнала-прототипа. В качестве одного из таких примеров мы рассмотрим один - поиск промоторов в ДНК