Генетические алгоритмы

Эти алгоритмы могут использоваться для поиска экстремума нелинейных функций с множественными локальными минимумами. Они имитируют адаптацию живых организмов к внешним условиям в ходе эволюции. Точнее, они моделируют эволюцию целых популяций организмов и поэтому требуют достаточно больших ресурсов памяти и высокой скорости вычислительных систем. Важным достоинством их является то, что они не накладывают никаках требований на вид минимизируемой функции (например, дифференцируемость). Поэтому их можно применять в случаях, когда градиентные методы не применимы.

Генетические алгоритмы используют соответствующую терминологию, конфигурации системы называют хромосомами, над которой можно производить операции кроссинговера и мутации. Хромосома является основной информационной единицей, кодирующей переменную, относительно которой ищется оптимум. Обычно она представляет собой битовую строку, хотя компоненты этой строки могут иметь и более общий вид (для задачи коммивояжера компоненты хромосом представляют собой последовательность номеров городов в данном маршруте, например (145321)). Каждая компонента хромосомы называется геном. Выбор удачного представления для хромосомы, или же кодировка искомого решения, могут значительно облегчить нахождение решения.

Обучение происходит в популяции хромосом, к которым на каждом шаге эволюции применяются две основные операции. При мутациях в хромосоме случайным образом выбираются и изменяются ее компоненты (гены). При кроссинговере две хромосомы А и В разрезаются на две части в случайно выбранной одной точке

и обмениваются ими, давая две новые хромосомы:

(см. рисунок 6.4).

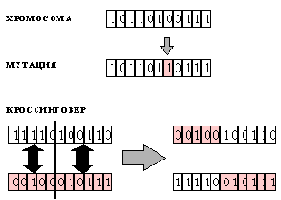
Рис. 6.4. Представление искомого решения в виде битовой строки - хромосомы (вверху). Операции мутации и кроссинговера (внизу)

После каждого шага эволюции - генерации, на котором мутируют и подвергаются кроссинговеру все хромосомы, для каждой из новых хромосом вычисляется значение целевого функционала, которое достигается на кодируемых ими решениях.
Чем меньше это значение для данной хромосомы, тем с большей вероятностью она отбираются для кроссинговера. В ходе эволюции усредненное по популяции значение функционала будет уменьшаться, и после завершения процесса (проведения заданного числа генераций) хромосома с минимальным его значаением выбирается в качестве приближенного решения поставленной задачи. Можно значительно улучшить свойства генетического алгоритма если после порождения новой генерации

хромосом предварительно объединить ее с предыдущей популяцией и выбрать из

полученных хромосом

наилучших. Опыт показывает, что генетические алгоритмы особенно эффективны при поиске глобального оптимума, поскольку они осуществляют поиск в широком пространстве решений. Если закодировать в виде хромосом значения весов и порогов нейронной сети заданной архитектуры и использовать в роли минимизируемой функции функционал ошибки, то генетические алгоритмы можно использовать для обучения этой нейронной сети. Очевидно, что для этой же цели можно использовать и описанный ранее метод иммитации отжига.

Содержание раздела