Растущие нейронные сети

Эффективное практическое применение нейронных сетей для оптимизации возможно, если вычислительные затраты у соответствующей модели не слишком быстро растут с ростом размерности задачи. Так, для задачи коммивояжера затраты при эмуляции сети Хопфилда на последовательном компьютере растут как

, т.к. каждый из

нейронов имеет порядка

синаптических

весов. 1)

Эвристический подход Лина и Кернигана масштабирует вычислительные затраты как

. Фритцке и Вильке предложили нейросетевую систему очень близкую к сети Кохонена, для которой затраты даже при ее эмуляции на последовательном компьютере растут лишь линейно с размерностью задачи (Fritzke & Wilke, 1991).

Предложенная ими модель относится к классу растущих нейронных сетей. Такие сети по-своему решают задачу адаптации своей структуры к требованиям решаемой задачи. Вспомним многослойные персептроны, для которых количества скрытых слоев и нейронов в них часто выбираются методом проб и ошибок. Как уже отмечалось в связи с этим, имеются два подхода к адаптивному выбору архитектуры нейросетей. В первом подходе заведомо избыточная нейросеть прореживается до нужной степени сложности. Растущие сети, напротив, стартуют с очень простых и небольших структур, которые разрастаются и усложняются по мере необходимости.

Фритцке и Вильке разработали целый класс самоорганизующихся (и обучаемых с учителем) сетей с изменяющейся структурой, такие как Растущие Клеточные Структуры, Растущий Нейронный Газ и Растущие Сетки. Первые и были использованы ими для решения задачи коммивояжера (и других задач комбинаторной оптимизации).

Растущая клеточная структура для задачи коммивояжера представляет из себя вначале кольцо из трех ячеек нейронов. Каждый нейрон характеризуется двумерным вектором

, определяющим его положение на плоскости. Каждому нейрону в кольце приписывается также своя величина погрешности

, которая вначале полагается равной нулю. Дальнейшая последовательность действий включает две следующие основные элементарные операции: смещение и добавление нового нейрона.
Смещение (см. рисунок 6.2)

выбирается случайный город
определяется нейрон-победитель
, ближайший к этому городу
положение нейрона
и его двух ближайших в кольце соседей смещается в сторону города
на определенную долю расстояния до него.

Эти операции очень близки к используемым в модели Кохонена. Различие состоит в том, что в последней радиус, в котором определяется соседство и параметр адаптации уменьшаются со временем.

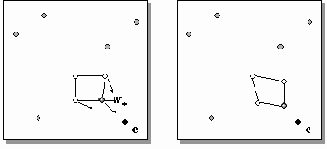
Рис. 6.2. Процедура смещения перемещает нейрон-победитель и его ближайших соседей в сторону случайно выбранного города

Содержание раздела