Индивидуальная нормировка данных

Приведение данных к единичному масштабу обеспечивается нормировкой каждой переменной на диапазон разброса ее значений. В простейшем варианте это - линейное преобразование:

в единичный отрезок:

. Обобщение для отображения данных в интервал

, рекомендуемого для входных данных тривиально.

Линейная нормировка оптимальна, когда значения переменной

плотно заполняют определенный интервал. Но подобный "прямолинейный" подход применим далеко не всегда. Так, если в данных имеются относительно редкие выбросы, намного превышающие типичный разброс, именно эти выбросы определят согласно предыдущей формуле масштаб нормировки. Это приведет к тому, что основная масса значений нормированной переменной

сосредоточится вблизи нуля:

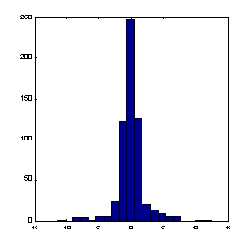
Рис. 7.2. Гистограмма значений переменной при наличии редких, но больших по амплитуде отклонений от среднего

Гораздо надежнее, поэтому, ориентироваться при нормировке не на экстремальные значения, а на типичные, т.е. статистические характеристики данных, такие как среднее и дисперсия:

В этом случае основная масса данных будет иметь единичный масштаб, т.е. типичные значения всех переменных будут сравнимы (см. рисунок 7.2).

Однако, теперь нормированные величины не принадлежат гарантированно единичному интервалу, более того, максимальный разброс значений

. заранее не известен. Для входных данных это может быть и не важно, но выходные переменные будут использоваться в качестве эталонов для выходных нейронов. В случае, если выходные нейроны - сигмоидные, они могут принимать значения лишь в единичном диапазоне. Чтобы установить соответствие между обучающей выборкой и нейросетью в этом случае необходимо ограничить диапазон изменения переменных.

Линейное преобразование, как мы убедились, неспособно отнормировать основную массу данных и одновременно ограничить диапазон возможных значений этих данных. Естественный выход из этой ситуации - использовать для предобработки данных функцию активации тех же нейронов. Например, нелинейное преобразование

нормирует основную массу данных одновременно гарантируя, что

(см. рисунок 7.3).

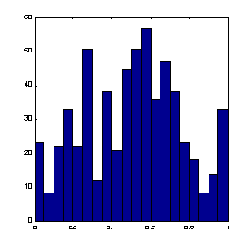
Рис. 7.3. Нелинейная нормировка, использующая логистическую функцию активации

Как видно из приведенного выше рисунка, распределение значений после такого нелинейного преобразования гораздо ближе к равномерному.

До сих пор мы старались максимизировать энтропию каждого входа (выхода) по отдельности. Но, вообще говоря, можно добиться гораздо большего максимизируя их совместную энтропию. Рассмотрим эту технику на примере совместной нормировки входов, подразумевая, что с таким же успехом ее можно применять и для выходов а также для всей совокупности входов-выходов.

Содержание раздела