Кодирование ординальных переменных

Ординальные переменные более близки к числовой форме, т.к. числовой ряд также упорядочен. Соответственно, для кодирования таких переменных остается лишь поставить в соответствие номерам категорий такие числовые значения, которые сохраняли бы существующую упорядоченность. Естественно, при этом имеется большая свобода выбора - любая монотонная функция от номера класса порождает свой способ кодирования. Какая же из бесконечного многообразия монотонных функций - наилучшая?

В соответствии с изложенным выше общим принципом, мы должны стремиться к тому, чтобы максимизировать энтропию закодированных данных. При использовании сигмоидных функций активации все выходные значения лежат в конечном интервале - обычно

или

. Из всех статистических функций распределения, определенных на конечном интервале, максимальной энтропией обладает равномерное распределение.

Применительно к данному случаю это подразумевает, что кодирование переменных числовыми значениями должно приводить, по возможности, к равномерному заполнению единичного интервала закодированными примерами. (Захватывая заодно и этап нормировки.) При таком способе "оцифровки" все примеры будут нести примерно одинаковую информационную нагрузку.

Исходя из этих соображений, можно предложить следующий практический рецепт кодирования ординальных переменных. Единичный отрезок разбивается на отрезков - по числу классов - с длинами пропорциональными числу примеров каждого класса в обучающей выборке:

, где

- число примеров класса

, а

, как обычно, общее число примеров. Центр каждого такого отрезка будет являться численным значением для соответствующего ординального класса (см. рисунок 7.1).

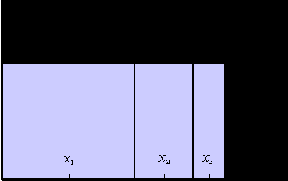
Рис. 7.1. Илюстрация способа кодирования кардинальных переменных с учетом количества примеров каждой категории

Содержание раздела