Линейная значимость входов

Легче всего оценить значимость входов в линейной модели, предполагающей линейную зависимость выходов от входов:

Матрицу весов

можно получить, например, обучением простейшего - однослойного персептрона с линейной функцией активации. Допустим теперь, что при определении выходов мы опускаем одну, для определенности -

-ю компоненту входов, заменяя ее средним значением этой переменной. Это приведет к огрублению модели, т.е. возрастании ошибки на величину:

(Полагая, что данные нормированны на их дисперсию.) Таким образом, значимость

-го входа определяется суммой квадратов соответствующих ему весов.

Особенно просто определить значимость выбеленных входов. Для достаточно просто вычислить взаимную корреляцию входов и выходов:

Действительно, при линейной зависимости между входами и выходами имеем:

Таким образом, в общем случае для получения матрицы весов требуется решить систему линейных уравнений. Но для предварительно выбеленных входов имеем:

, так что в этом случае матрица кросс-корреляций просто совпадает с матрицей весов обученного линейного персептрона:

Резюмируя, значимость входов в предположении о приблизительно линейной зависимости между входными и выходными переменными для выбеленных входов пропорциональна норме столбцов матрицы кросс-корреляций:

Не следует, однако, обольщаться существованием столь простого рецепта определения значимости входов. Линейная модель может быть легко построена и без привлечения нейросетей. Реальная сила нейроанализа как раз и состоит в возможности находить более сложные нелинейные зависимости. Более того, для облегчения собственно нелинейного анализа рекомендуется заранее освободиться от тривиальных линейных зависимостей - т.е. в качестве выходов при обучении подавать разность между выходными значениями и их линейным приближением. Это увеличит "разрешающую способность" нейросетевого моделирования (см. рисунок 7.12).

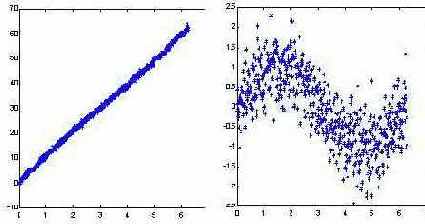
Рис. 7.12. Выявление нелинейной составляющей функции после вычитания линейной зависимости . ( Здесь - гауссовый случайный шум)

Для определения "нелинейной" значимости входов - после вычитания линейной составляющей, изложенный выше подход неприменим. Здесь надо привлекать более изощренные методики. К описанию одной из них, алгоритмам box-counting, мы и переходим.

Содержание раздела