Метод погружения. Теорема Такенса

Начнем с этапа погружения. Как мы сейчас убедимся, несмотря на то, что предсказания, казалось бы, являются экстраполяцией данных, нейросети, на самом деле, решают задачу интерполяции, что существенно повышает надежность решения. Предсказание временного ряда сводится к типовой задаче нейроанализа - аппроксимации функции многих переменных по заданному набору примеров - с помощью процедуры погружения ряда в многомерное пространство (Weigend, 1994). Например,

-мерное лаговое пространство ряда

состоит из

значений ряда в последовательные моменты времени:

Для динамических систем доказана следующая теорема Такенса. Если временной ряд порождается динамической системой, т.е. значения

есть произвольная функция состояния такой системы, существует такая глубина погружения

(примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда (Sauer, 1991). Таким образом, выбрав достаточно большое

можно гарантировать однозначную зависимость будущего значения ряда от его

предыдущих значений:

, т.е. предсказание временного ряда сводится к задаче интерполяции функции многих переменных. Нейросеть далее можно использовать для восстановления этой неизвестной функции по набору примеров, заданных историей данного временного ряда.

Напротив, для случайного ряда знание прошлого ничего не дает для предсказания будущего. Поэтому, согласно теории эффективного рынка, разброс предсказываемых значений ряда на следующем шаге при погружении в лаговое пространство не изменится.

Отличие хаотической динамики от стохастической (случайной), проявляющееся в процессе погружения, иллюстрирует рисунок 8.2.

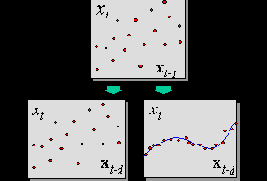
Рис. 8.2. Проявляющееся по мере погружения ряда различие между случайным процессом и хаотической динамикой

Содержание раздела