Связь предсказуемости с нормой прибыли

Особенностью предсказния финансовых временных рядов является стремление к получению максимальной прибыли, а не минимизации среднеквадратичного отклонения, как это принято в случае аппроксимации функций.

В простейшем случае ежедневной торговли прибыль зависит от верно угаданого знака изменения котировки. Поэтому нейросеть нужно ориентировать именно на точность угадывания знака, а не самого значения. Найдем как связана норма прибыли с точностью определения знака в простейшей постановке ежедневного вхождения в рынок ( рисунок 8.9).

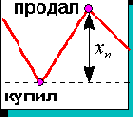
Рис. 8.9. Ежедневное вхождение в рынок

Обозначим на момент

: полный капитал игрока

, относительное изменение котировки

, а в качестве выхода сети возьмем степень ее уверенности в знаке этого изменения

. Такая сеть с выходной нелинейностью вида

обучается предсказывать знак изменения и выдает прогноз знака с амплитудой пропорциональной его вероятности. Тогда возрастание капитала на шаге

запишется в виде:

где

- доля капитала, "в игре". Выигрыш за все время игры:

нам и предстоит максимизировать, выбрав оптимальный размер ставок

. Пусть в среднем игрок угадывает долю

знаков и, соответственно, ошибается с вероятностью

. Тогда логарифм нормы прибыли,

а следовательно и сама прибыль, будет максимальным при значении

и составит в среднем:

Здесь мы ввели коэффициент

. Например, для Гауссова распределения

. Степень предсказуемости знака напрямую связана с кросс-энтропией, которую можно оценить a priory методом box-counting. Для бинарного выхода (см. рисунок 8.10):

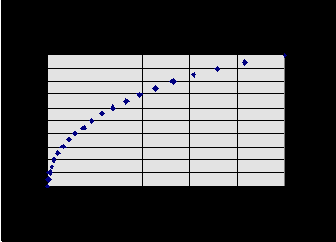
Рис. 8.10. Доля правильно угаданных направлений изменений ряда как функция кросс-энтропии знака выхода при известных входах

В итоге получаем следующую оценку нормы прибыли при заданной величине предсказуемости знака

, выраженной в битах:

То есть, для ряда с предсказуемостью

в принципе возможно удвоить капитал за

вхождений в рынок. Так, например, измеренная выше предсказуемость временного ряда S&P500, равная

(см.
рисунок 8.8) предполагает удвоение капитала в среднем за

вхождений в рынок. Таким образом, даже небольшая предсказуемость знака изменения котировок способна обеспечить весьма заметную норму прибыли.

Подчеркнем, что оптимальная норма прибыли требует достаточно аккуратной игры, когда при каждом вхождении в рынок игрок рискует строго определенной долей капитала:

где

- типичная при данной волатильности рынка

величина выигрыша или

проигрыша. 1) Как меньшие, так и большие значения ставок уменьшают прибыль. Причем, чересчур рискованная игра может привести к проигрышу при любой предсказательной способности. Этот факт иллюстрирует рисунок 8.11.

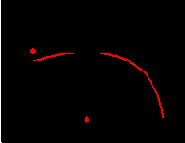
Рис. 8.11. Зависимость средней нормы прибыли от выбора доли капитала "на кону"

Поэтому приведенные выше оценки дают представление лишь о верхнем пределе нормы

прибыли. 2)

Более тщательный анализ с учетом влияния флуктуаций, выходит за рамки нашего изложения. Качественно понятно, однако, что выбор оптимального размера контрактов требует оценки точности предсказаний на каждом шаге.

Содержание раздела