Нейрокомпьютинг и его применения в экономике и бизнесе
Извлечение правил
Даже если параметры, описывающие признаки классифицируемых объектов, представляют собой непрерывные величины, для их представления можно использовать бинарные нейроны и принцип кодирования типа термометра. При таком способе кодирования область изменения параметра делится на конечное число
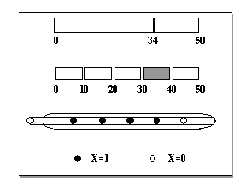
Рис. 9.1. . Пример кодировки непрерывной величины с помощью бинарных нейронов и принципа термометра. Интервал (0, 50) разбит на 5 равных частей. Значение 34.0 попадает в 4-й интервал. При этом состояния первых 4 из 5 кодирующих бинарных нейронов равно единице, а 5-го - нулю.
При наличии многих непрерывных входов число заменяющих их бинарных нейронов может стать весьма большим. Однако, прореживание связей приводит к получению относительно ком-пактной сети. Но и для нее выделение классификационных правил представляет проблему. Если нейрон имеет d входов, то число различных бинарных векторов, которые он может обра-ботать составляет
Алгоритм дискретизации
- Выбирается значение параметра , управляющего числом кластеров активности нейрона скрытого слоя. Пусть
- активность этого нейрона при предъявлении сети первого вектора обучающего набора. Положим число кластеров
, положение кластера
.
- Для всех векторов обучающего набора
- определяется активность нейрона скрытого слоя
- если существует индекс такой что
и
тоиначе
- определяется активность нейрона скрытого слоя
- Заменить на среднее значение активаций нейрона, объединенных в один и тот же кластер:
.
- Проверить точность классификации объектов сетью при замене истинных значений активации нейрона скрытого слоя на .
- Если точность классификации оказалась ниже заданного значения, то уменьшить значение и вернуться к шагу 1.
Рассмотрим приведенный в (Lu, Setiono and Liu, 1995) пример, в котором прореженная сеть содержала три нейрона скрытого слоя, дискретизация активности которых была проведена при значении параметра
| 1 | 3 | (-1,0,1) |
| 2 | 2 | (0, 1) |
| 3 | 3 | (-1, 0.24, 1) |
В этой работе решалась задача разбиения объектов на два класса. На ее примере мы и рассмотрим последовательность извлечения правил. После дискретизации значений активности нейронов скрытого слоя, передача их воздействий выходным классифицирующим нейронам описывалась параметрами, приведенными в таблице 9.2.
| -1 | 1 | -1 | 0.92 | 0.08 |
| -1 | 1 | 1 | 0.00 | 1.00 |
| -1 | 1 | 0.24 | 0.01 | 0.99 |
| -1 | 0 | -1 | 1.00 | 0.00 |
| -1 | 0 | 1 | 0.11 | 0.89 |
| -1 | 0 | 0.24 | 0.93 | 0.07 |
| 1 | 1 | -1 | 0.00 | 1.00 |
| 1 | 1 | 1 | 0.00 | 1.00 |
| 1 | 1 | 0.24 | 0.00 | 1.00 |
| 1 | 0 | -1 | 0.89 | 0.11 |
| 1 | 0 | 1 | 0.00 | 1.00 |
| 1 | 0 | 0.24 | 0.00 | 1.00 |
| 0 | 1 | -1 | 0.18 | 0.82 |
| 0 | 1 | 1 | 0.00 | 1.00 |
| 0 | 1 | 0.24 | 0.00 | 1.00 |
| 0 | 0 | -1 | 1.00 | 0.00 |
| 0 | 0 | 1 | 0.00 | 1.00 |
| 0 | 0 | 0.24 | 0.18 | 0.82 |
Исходя из значений, приведенных в этой таблице, после замены значений выходных нейронов ближайшими к ним нулями или единицами, легко получить следующие правила, связывающие активности нейронов скрытого слоя с активностями классифицирующих нейронов
- правило 1 если h2=0,h3=-1, то o1=1, o2=0 (объект класса А)
- правило 2 если h1=-1,h2=1,h3=-1, то o1=1, o2=0 (объект класса А)
- правило 3 если h1=-1,h2=0,h3=0.24, то o1=1, o2=0 (объект класса А)
- правило 4 в остальных случаях o1=1, o2=0 (объект класса В)
Эти правила являются вспомогательными, поскольку нам необходимо связать значения состояний классифицирующих выходных нейронов со входами нейронной сети. Структура данной сети после прореживания связей и нейронов изображена на следующем рисунке.
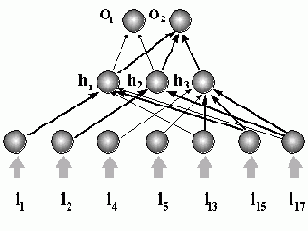
Рис. 9.2. Двухслойная сеть после прореживания связей и входных нейронов. Положительные связи выделены.
Связь между активностями входных бинарных нейронов и нейронов скрытого слоя для данной сети определяется следующими правилами:
Для первого нейрона скрытого слоя:
Для второго нейрона скрытого слоя:
Для третьего нейрона скрытого слоя:
Комбинируя эти связи с правилами, связывающими активности нейронов скрытого слоя с ак-тивностями выходных нейронов, получим окончательные классифицирующие правила.
Приведенные выше правила определяют принадлежность объекта первому классу (А). Некото-рые из них могут оказаться нереализуемыми, если учесть, что состояния бинарных нейронов кодируют соответствующие непрерывные величины с помощью принципа термометра.
Количество правил, полученных в данном случае, невелико. Однако, иногда даже после проце-дуры прореживания некоторые нейроны скрытого слоя могут иметь слишком много связей с входными нейронами. В этом случае извлечение правил становится нетривиальным, а если оно и осуществлено, то полученные правила не так просто понять. Для выхода из этой ситуации для каждого из "проблемных" нейронов скрытого слоя можно использовать вспомогательные двух-слойные нейронные сети. Во вспомогательной сети количество выходных нейронов равно чис-лу дискретных значений соответствующего "проблемного" нейрона скрытого слоя, а входными нейронами являются те, которые в исходной прореженной сети связаны с данным нейроном скрытого слоя.
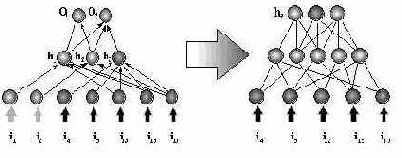
Рис. 9.3. . Третий нейрон скрытого слоя связан с максимальным числом входов. Число дискретных значений его активности равно 3. Для облегчения процедуры выделения классифицирующих правил этот нейрон может быть заменен вспомогательной сетью с тремя выходными нейронами, кодирующими дискретные значения активности.
Обучающие примеры для вспомогательной сети группируются согласно их дискретизованным значениям активации "проблемного" нейрона.
Для
