Примеры сетевых топологий
Ориентированные и неориентированные сети
Общий метод преобразования неориентированного ребра в пару противоположно ориентированных ребер проиллюстрирован на рис. 2. Этот подход широко применяется в задачах сетевой надежности.
Теорема 2.1. Пусть дан неориентированный граф G=(V,E), заданы вероятности разрыва ребер, их функция распределение по длинам {lе,i, pе,i } или по пропускной способности {се,i, pе,i}. Применяя схему на рисунке 2 к каждому ребру исходного графа, получен ориентированный граф Gў=(V,A), надежность ориентированных дуг равна pa, а распределение по длинам {la,i, pa,i} или по пропускной способности {сa,i, pa,i}. Если эти параметры окажутся равными соответствующим параметрам неориентированного графа, тогда справедливо:
Rel(G,s,K,p) = Rel(Gў,s,K,{pa})
FT(G,s,t,{се,i},{ pе,i},fthresh) = FT(Gў,s,t,{сa,i}, {pa,i},fthresh)
ST(G,s,t,{dе,i }, { pе,i},lthresh) = FT(Gў,s,t,{da,i}, {pa,i},lthresh)
FE(G,s,t,{се,i}, {pе,i }) = FT(Gў,s,t,{сa,i}, {pa,i})
SE(G,s,t,{dе,i}, {pе,i}) = FT(Gў,s,t,{da,i}, {pa,i})
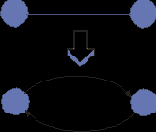
Рис. 2. Преобразование неориентированных графов в диграфы.
Рассмотренное преобразование идентично тем преобразованиям, что применяются для сетевых потоков. Теорема 2.1 дает нам право трактовать состояния антипараллельной пары дуг, как пару независящих друг от друга случайных величин, в то время как их состояния не являются независимыми. Полученные соотношения могут не выполняться, если рассматривать более сложные меры работоспособности.