Примеры сетевых топологий
Основные определения
Из-за отсутствия приемлемой модели механизма потерь в сети и присущей сложности расчета сетевой надежности используются времязависимые модели с дискретной вероятностью. В статье мы рассмотрим наиболее популярную модель, в ней предполагается, что сетевые компоненты (узлы и ребра на языке графов) могут принимать лишь два состояния: работает или не работает. Состояние сетевого компонента - случайная величина, не зависящая от состояния других компонентов (в общем случае это может быть и не так). Постановка задачи вычисления надежности: для каждого компонента сети задана вероятность того, что он находится в рабочем состоянии, требуется вычислить меру надежности сети. Рассмотрим некое обобщение этой модели. В частности, будем рассматривать модели, в которых каждый компонент может находиться в одном из нескольких состояний, или модели, в которых рабочее состояние характеризуется численным значением. Численные значения этих характеристик обычно приравниваются метрике расстояния или величине пропускной способности. Простая модель с двумя состояниями хорошо подходит для вычисления меры связанности. Когда возникает необходимость посчитать более сложную меру, например производительность системы, применяют более сложные характеристики состояний компонентов.
Для модели с двумя состояниями вероятность работоспособности компонента или, проще надежность, можно понимать по-разному. Наиболее распространенными являются формулировки:
1. доступность компонента
2. надежность компонента
Вообще в этой главе договоримся применять термин надежность для обозначения вероятности того, что компонент или система работает. Здесь мы обсуждаем более частное определение. Доступность используется в контексте ремонтоспособных систем. Из сказанного следует, что компонент может находиться в одном из трех состояний: работает, не работает, в процессе восстановления. Доступность компонента определяется как вероятность его работы в случайный момент времени. Оценка величины доступности производится с учетом среднего времени восстановления в рабочее состояние и среднего времени в не рабочем состоянии.
Надежность можно записать:
среднее время до отказа
среднее время до отказа + среднее время восстановления.
Определение надежности компонента не учитывает время восстановления. Специфицируется промежуток времени t, а надежность компонента определяется как вероятность того, что за это время t компонент останется в рабочем состоянии. Допускаются также иные трактовки для вероятности того, что компонент работает. Конечно, интерпретация уровня надежности компонента определяет в свою очередь интерпретацию мер сетевой надежности. В оставшейся части статьи мы будем использовать вероятность работоспособности или надежности и не будем пытаться это как-либо интерпретировать.
За отправную точку примем сеть G=(V,E), в которой V - набор узлов или вершин, а Е - набор неориентированных ребер или набор ориентированных дуг. При изучении моделей связанности для каждого еОЕ мы определяем надежность е (ре) как Pr[e работает]. При изучении простых моделей потоков (кратчайших путей), мы ассоциируем пропускную способность се(расстояние dе) с каждым еОЕ. Мы интерпретируем ре, как вероятность того, что е работает и имеет пропускную способность се (расстояние dе), а 1-ре, как вероятность того, что е не работает и имеет пропускную способность 0 (расстояние равно бесконечности). При изучении моделей потоков (кратчайших путей) с множеством состояний мы ассоциируем распределение пропускной способности {cе,i, pе,i} (распределение расстояний {dе,i, pе,i}) для еОЕ. Здесь pе,i - вероятность того, что е будет иметь пропускную способность cе,i (расстояние dе,i).
Иногда, при изучении сетевой надежности, бывает удобно переходить к обобщенным случаям и рассматривать когерентные двоичные системы. Стохастическая бинарная система SBS (stochastic binary system) - представляет собой систему, которая отказывает случайным образом в результате случайного выхода из строя ее компонента. Каждый компонент из набора сетевых компонентов T может принимать одно из двух значений: работает, не работает. Структура системы описывается функцией ? (S), определенной для SНT.
? (S)=
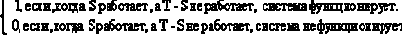
Функция SBS является когерентной, если ?(Т)=1, ?(0)=0 и выполняется условие ?(S?)??(S) для S?ЙS. Последнее свойство означает, что выход из строя любого из компонентов может только повредить работе системы. Представляет интерес задача вычисления выражения:
Rel(SBS,p)=Pr[?(S)=1, где S - набор работающих компонентов],
если известен вид распределения ?(). Иногда мы рассматриваем задачи надежности, где ре=p для всех е, в этих случаях мы заменяем p на p в представленной выше нотации. Для произвольной стохастической когерентной двоичной системы (SCBS - stochastic coherent binary system) определим набор путей как набор компонентов, работоспособность которых означает работу системы в целом. Назовем минипроходом - минимальный набор путей, обеспечивающих работоспособность системы. Аналогично определим набор разрезов, как набор компонентов, чей отказ вызовет отказ системы, а миниразрезом назовем минимальный набор таких разрезов.