Примеры сетевых топологий
Отказы узлов
Во многих приложениях могут отказывать как дуги, так и узлы. Следовательно, приходится изучать модели, способные реагировать и на отказы узлов и на обрывы дуг. К счастью, для случая ориентированных сетей с помощью преобразования, показанного на рисунке 3, задачу с ненадежными ребрами и узлами можно свести к задаче с абсолютно надежными узлами и ненадежными ребрами. Преобразование используется для мер Rel(), FT(), ST(), FE() и SE(), где в каждом случае дуга, которая замещает узлы, наследует характеристики соответствующих узлов. При осуществлении преобразования для терминального узла i узел-заменитель i1 не должен быть терминальным, а узел-заменитель i2 должен быть терминальным. При выполнении этого преобразования для исходящего узла i нужно, чтобы i1 был исходящим, а i2 - таковым не был.
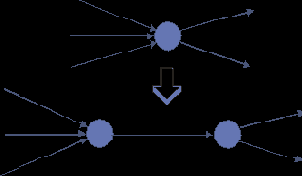
Рис. 3. Замена ненадежного узла.
Теорема 2.1 и выше представленное обсуждение указывают, что с практической точки зрения предпочтительнее коды для анализа надежности ориентированной сети по отношению к кодам для неориентированного случая. При условии тщательного подбора входных данных, ориентированные сетевые коды можно применять для анализа ориентированных и неориентированных моделей сети и задач с отказом узлов и без.